Exercise 6.6

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

%matplotlib inline

(a)

For p = 1, (6.12) takes the form: $(y-\beta)^2 + \lambda \beta^2$ .

# Random variables
np.random.seed(1)
y1 = np.random.randint(low=1, high=10)
lamb = np.random.randint(low=1, high=10)

# Functions
beta = np.arange(-10,10,.1)
y = (y1 - beta)**2 + lamb*beta**2 

min_beta = y1/(1+lamb)
y_min = (y1 - min_beta)**2 + lamb*min_beta**2

# Plot
plt.scatter(beta,y);
plt.plot(min_beta, y_min, 'ro');

png

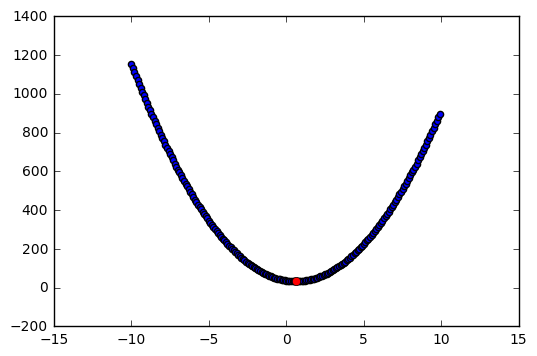
As we can see, the point that corresponds to (6.14) solves (6.12). By other words, the point resulting from (6.14) is the point that minimizes the ridge regression.

(b)

For p = 1, (6.12) takes the form: $(y-\beta)^2 + \lambda |\beta|$ .

# Case 1: y1 > lamb/2
y1 = 6
lamb = 4

# Functions
beta = np.arange(-10,10,.1)
y = (y1 - beta)**2 + lamb*abs(beta)

min_beta = y1 - (lamb/2)
y_min = (y1 - min_beta)**2 + lamb*abs(min_beta)

# Plot 
plt.scatter(beta,y)
plt.plot(min_beta, y_min, 'ro');

png

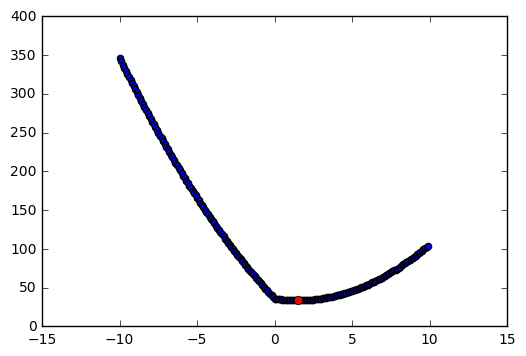
# Case 1: y1 < -lamb/2
y1 = -6
lamb = 4

# Functions
beta = np.arange(-10,10,.1)
y = (y1 - beta)**2 + lamb*abs(beta)

min_beta = y1 + (lamb/2)
y_min = (y1 - min_beta)**2 + lamb*abs(min_beta)

# Plot 
plt.scatter(beta,y)
plt.plot(min_beta, y_min, 'ro');

png

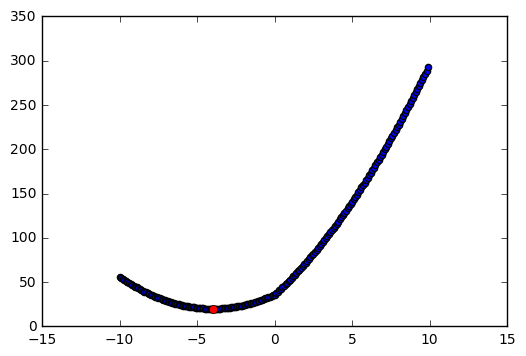
# Case 3: |y1| <= lamb/2
y1 = -2
lamb = 4

# Functions
beta = np.arange(-10,10,.1)
y = (y1 - beta)**2 + lamb*abs(beta)

min_beta = 0
y_min = (y1 - min_beta)**2 + lamb*abs(min_beta)

# Plot 
plt.scatter(beta,y)
plt.plot(min_beta, y_min, 'ro');

png

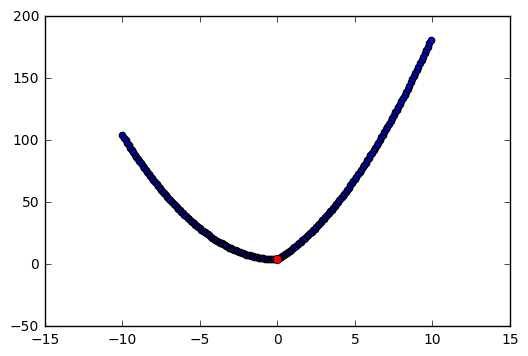
As we can see in the figures above, (6.13) is solved by (6.15). This means that (6.15) minimizes the lasso estimates.