Exercise 10.10
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import scale
%matplotlib inline
(a)
# Generate dataset
# scikit-learn includes various random sample generators that can be used to build artificial datasets of controlled size and complexity.
# make_blobs provides greater control regarding the centers and standard deviations of clusters, and is used to demonstrate clustering.
X, y = make_blobs(n_samples=60, n_features=50, centers=3, cluster_std=5, random_state=1)
(b)
# PCA
# We are looking for the first two principal components, so n_components=2.
pca = PCA(n_components=2, random_state=1)
X_r = pca.fit_transform(X)
# Plot
plt.figure()
colors = ['blue', 'red', 'green']
for color, i in zip(colors, [0,1,2]):
plt.scatter(X_r[y==i, 0], X_r[y==i, 1], color=color)
plt.title('Principal component score vectors')
plt.xlabel('First principal component')
plt.ylabel('Second principal component')
<matplotlib.text.Text at 0x10941eb8>
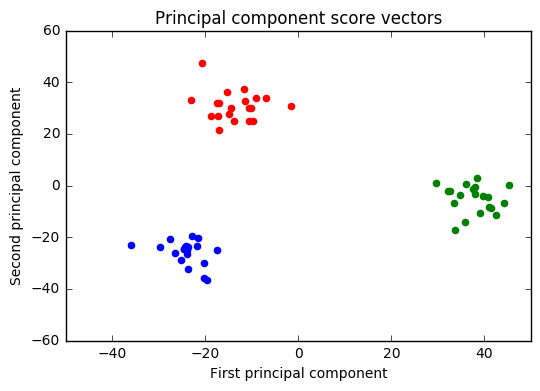
(c)
# Get clustering labels using K-means
km3 = KMeans(n_clusters=3)
km3.fit(X)
km3.labels_
array([2, 0, 1, 0, 0, 0, 2, 2, 2, 0, 0, 0, 2, 0, 1, 2, 1, 1, 2, 0, 2, 0, 1,
2, 2, 1, 1, 1, 2, 0, 1, 0, 2, 1, 0, 1, 1, 1, 1, 0, 1, 1, 2, 0, 0, 2,
2, 2, 0, 2, 0, 0, 1, 1, 2, 1, 2, 0, 1, 2])
# Get true class labels
y
array([0, 1, 2, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 2, 0, 2, 2, 0, 1, 0, 1, 2,
0, 0, 2, 2, 2, 0, 1, 2, 1, 0, 2, 1, 2, 2, 2, 2, 1, 2, 2, 0, 1, 1, 0,
0, 0, 1, 0, 1, 1, 2, 2, 0, 2, 0, 1, 2, 0])
The results show an agreement between true class labels and clustering labels. K-means clustering will arbitrarily number the clusters, so we cannot simply check whether the true class labels and clustering labels are the same. Here, the arbitrary attribution of numbers to the clusters led to the following correspondences:
- Clustering label 0 --> true class label 1.
- Clustering label 1 --> true class label 2.
- Clustering label 2 --> true class label 0.
Considering these correspondences, we can see that both labels match perfectly.
(d)
# Get clustering labels using K-means
km3 = KMeans(n_clusters=2)
km3.fit(X)
km3.labels_
array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1,
0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0])
# Get true class labels
y
array([0, 1, 2, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 2, 0, 2, 2, 0, 1, 0, 1, 2,
0, 0, 2, 2, 2, 0, 1, 2, 1, 0, 2, 1, 2, 2, 2, 2, 1, 2, 2, 0, 1, 1, 0,
0, 0, 1, 0, 1, 1, 2, 2, 0, 2, 0, 1, 2, 0])
In this case, we only have two clustering labels. The results above show that when:
- Clustering label is 0 --> true class label can be 0 or 1.
- Clustering label is 1 --> true class label is 2;
This means that when K-means is equal to 2, we are merging the labels 0 and 1. Thus, we can say that label 2 corresponds to a finer set of observations.
(e)
# Get clustering labels using K-means
km3 = KMeans(n_clusters=4)
km3.fit(X)
km3.labels_
array([2, 0, 1, 0, 0, 0, 2, 2, 2, 0, 0, 0, 2, 0, 3, 2, 3, 3, 2, 0, 2, 0, 3,
2, 2, 3, 1, 1, 2, 0, 3, 0, 2, 3, 0, 1, 1, 3, 1, 0, 3, 3, 2, 0, 0, 2,
2, 2, 0, 2, 0, 0, 1, 3, 2, 1, 2, 0, 1, 2])
# Get true class labels
y
array([0, 1, 2, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 2, 0, 2, 2, 0, 1, 0, 1, 2,
0, 0, 2, 2, 2, 0, 1, 2, 1, 0, 2, 1, 2, 2, 2, 2, 1, 2, 2, 0, 1, 1, 0,
0, 0, 1, 0, 1, 1, 2, 2, 0, 2, 0, 1, 2, 0])
The results show the following correspondences between clustering and true labels:
- Clustering label 0 --> True label 2.
- Clustering label 1 --> True label 1.
- Clustering label 2 --> True label 0.
- Clustering label 3 --> True label 1.
We can conclude that the original cluster 1 (true label = 1), was split into two different clusters (clustering labels 1 and 3). The remaining clusters didn't have any significant change. This is an expected result, since the only coherent way to create a new cluster would be to split one of the original clusters, while remaining the other two unchanged.
(f)
# Get clustering labels using K-means
km3 = KMeans(n_clusters=3)
km3.fit(X_r)
km3.labels_
array([2, 0, 1, 0, 0, 0, 2, 2, 2, 0, 0, 0, 2, 0, 1, 2, 1, 1, 2, 0, 2, 0, 1,
2, 2, 1, 1, 1, 2, 0, 1, 0, 2, 1, 0, 1, 1, 1, 1, 0, 1, 1, 2, 0, 0, 2,
2, 2, 0, 2, 0, 0, 1, 1, 2, 1, 2, 0, 1, 2])
# Get true class labels
y
array([0, 1, 2, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 2, 0, 2, 2, 0, 1, 0, 1, 2,
0, 0, 2, 2, 2, 0, 1, 2, 1, 0, 2, 1, 2, 2, 2, 2, 1, 2, 2, 0, 1, 1, 0,
0, 0, 1, 0, 1, 1, 2, 2, 0, 2, 0, 1, 2, 0])
The results show that, apart from the correspondences, true and clustering labels match perfectly. This means that the two principal components were able to reduce dimensionsal space without loss of information.
(g)
# Scale variables
# Data will be scaled to unit variance but it will not be centered (mean will not be removed).
X_scaler = StandardScaler(with_mean=False)
X_scl = X_scaler.fit_transform(X)
# Get clustering labels using K-means
km3 = KMeans(n_clusters=3)
km3.fit(X_scl)
km3.labels_
array([0, 2, 1, 2, 2, 2, 0, 0, 0, 2, 2, 2, 0, 2, 1, 0, 1, 1, 0, 2, 0, 2, 1,
0, 0, 1, 1, 1, 0, 2, 1, 2, 0, 1, 2, 1, 1, 1, 1, 2, 1, 1, 0, 2, 2, 0,
0, 0, 2, 0, 2, 2, 1, 1, 0, 1, 0, 2, 1, 0])
# Get true class labels
y
array([0, 1, 2, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 2, 0, 2, 2, 0, 1, 0, 1, 2,
0, 0, 2, 2, 2, 0, 1, 2, 1, 0, 2, 1, 2, 2, 2, 2, 1, 2, 2, 0, 1, 1, 0,
0, 0, 1, 0, 1, 1, 2, 2, 0, 2, 0, 1, 2, 0])
As in the previous cases, apart from the correspondence between clustering and true class, the labels match perfectly. However, it should be noted that this is not an obvious result. The k-means algorithm is sensitive to the scale of the variables. Standardizing the observations can have a strong impact on the results obtained. Accordingly, it could have happened that the clustering and the true class didn't match.
The decision about standardizing or not the variables depends on the data. In a real case, we should look for different choices and go for the one that give us the most interpretable solution or the most useful solution.