Exercise 3.10
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import statsmodels.formula.api as smf #statsmodels is a Python module for statistics
%matplotlib inline
url = 'https://raw.github.com/vincentarelbundock/Rdatasets/master/csv/ISLR/Carseats.csv '
df = pd.read_csv(url,index_col=0)
df.head()
| Sales | CompPrice | Income | Advertising | Population | Price | ShelveLoc | Age | Education | Urban | US | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 9.50 | 138 | 73 | 11 | 276 | 120 | Bad | 42 | 17 | Yes | Yes |
| 2 | 11.22 | 111 | 48 | 16 | 260 | 83 | Good | 65 | 10 | Yes | Yes |
| 3 | 10.06 | 113 | 35 | 10 | 269 | 80 | Medium | 59 | 12 | Yes | Yes |
| 4 | 7.40 | 117 | 100 | 4 | 466 | 97 | Medium | 55 | 14 | Yes | Yes |
| 5 | 4.15 | 141 | 64 | 3 | 340 | 128 | Bad | 38 | 13 | Yes | No |
(a)
# fit regression model
mod = smf.ols(formula='Sales ~ Price + Urban + US',data=df)
res = mod.fit()
res.summary()
| Dep. Variable: | Sales | R-squared: | 0.239 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.234 |
| Method: | Least Squares | F-statistic: | 41.52 |
| Date: | Fri, 08 Dec 2017 | Prob (F-statistic): | 2.39e-23 |
| Time: | 09:49:21 | Log-Likelihood: | -927.66 |
| No. Observations: | 400 | AIC: | 1863. |
| Df Residuals: | 396 | BIC: | 1879. |
| Df Model: | 3 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 13.0435 | 0.651 | 20.036 | 0.000 | 11.764 | 14.323 |
| Urban[T.Yes] | -0.0219 | 0.272 | -0.081 | 0.936 | -0.556 | 0.512 |
| US[T.Yes] | 1.2006 | 0.259 | 4.635 | 0.000 | 0.691 | 1.710 |
| Price | -0.0545 | 0.005 | -10.389 | 0.000 | -0.065 | -0.044 |
| Omnibus: | 0.676 | Durbin-Watson: | 1.912 |
|---|---|---|---|
| Prob(Omnibus): | 0.713 | Jarque-Bera (JB): | 0.758 |
| Skew: | 0.093 | Prob(JB): | 0.684 |
| Kurtosis: | 2.897 | Cond. No. | 628. |
(b)
Interpretation Urban. This coefficient is not statistically significant, suggesting that there is no relationship between this variable and the sales. US. Qualitative variable with positive relationship. This means that when the observation is US, there will be a tendency for higher sales values. On average, if a store is located in the US, it will sell 1201 more units, approximately. * Price. Quantitative variable with negative relationship. This means that the higher the prices, the lower the sales. On average, for every dollar that the price increases sales will drop by 55 units, approximately.
# (c)
(d)
From the p-values in the summary above, we can reject the null hypothesis for the intercept, US and Price, but not for Urban.
(e)
mod = smf.ols(formula='Sales ~ Price + US',data=df)
res = mod.fit()
print(res.summary())
OLS Regression Results
==============================================================================
Dep. Variable: Sales R-squared: 0.239
Model: OLS Adj. R-squared: 0.235
Method: Least Squares F-statistic: 62.43
Date: Fri, 08 Dec 2017 Prob (F-statistic): 2.66e-24
Time: 09:49:21 Log-Likelihood: -927.66
No. Observations: 400 AIC: 1861.
Df Residuals: 397 BIC: 1873.
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 13.0308 0.631 20.652 0.000 11.790 14.271
US[T.Yes] 1.1996 0.258 4.641 0.000 0.692 1.708
Price -0.0545 0.005 -10.416 0.000 -0.065 -0.044
==============================================================================
Omnibus: 0.666 Durbin-Watson: 1.912
Prob(Omnibus): 0.717 Jarque-Bera (JB): 0.749
Skew: 0.092 Prob(JB): 0.688
Kurtosis: 2.895 Cond. No. 607.
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
(f)
To compare how well the models fit, we can consider the value of R-squared. R-squared is the coefficient of determination. The coefficient of determination measures how much of the variance can be explained by the independent variables considered in the model.
Since R-squared has the same value, namely 0.239, for both models we can conclude that the strictly smaller model (e), is a better model since it uses less variables for the same value of R-squared. This can also be seen in the value of the adjusted R-squared which is smaller for (e). In any case neither model fits the data very well given the low value of R-squared.
(g)
For linear regression, the 95% confidence interval for the coefficients approximately takes the form:
where SE is the standard error of the coefficient \hat{\beta}.
# confidence interval for intercept
intercept_coef = 13.0308
intercept_stderr = .631
us_coef = 1.1996
us_stderr = .258
price_coef = -.0545
price_stderr = .005
print('95%% confidence interval for Intercept: [ %2.4f; %2.4f] ' % (intercept_coef-2*intercept_stderr, intercept_coef+2*intercept_stderr))
print('95%% confidence interval for Intercept: [ %2.4f; %2.4f] ' % (us_coef-2*us_stderr, us_coef+2*us_stderr))
print('95%% confidence interval for Intercept: [ %2.4f; %2.4f] ' % (price_coef-2*price_stderr, price_coef+2*price_stderr))
95% confidence interval for Intercept: [ 11.7688; 14.2928]
95% confidence interval for Intercept: [ 0.6836; 1.7156]
95% confidence interval for Intercept: [ -0.0645; -0.0445]
As we can check this does not precisely equal the values in the summary table above. This is because of the approximation mentioned in the footnote on page 66 of the text.
(h)
To investigate the presence of outliers or high leverage points, we analyse a plot of standardized residuals against leverages.
import statsmodels.formula.api as smf
from statsmodels.graphics.gofplots import ProbPlot
plt.style.use('seaborn') # pretty matplotlib plots
plt.rc('font', size=14)
plt.rc('figure', titlesize=18)
plt.rc('axes', labelsize=15)
plt.rc('axes', titlesize=18)
model_f = 'Sales ~ Price + US'
df.reset_index(drop=True, inplace=True)
model = smf.ols(formula=model_f, data=df)
model_fit = model.fit()
# fitted values (need a constant term for intercept)
model_fitted_y = model_fit.fittedvalues
# model residuals
model_residuals = model_fit.resid
# normalized residuals
model_norm_residuals = model_fit.get_influence().resid_studentized_internal
# absolute squared normalized residuals
model_norm_residuals_abs_sqrt = np.sqrt(np.abs(model_norm_residuals))
# absolute residuals
model_abs_resid = np.abs(model_residuals)
# leverage, from statsmodels internals
model_leverage = model_fit.get_influence().hat_matrix_diag
# cook's distance, from statsmodels internals
model_cooks = model_fit.get_influence().cooks_distance[0]
plot_lm_4 = plt.figure(4)
plot_lm_4.set_figheight(8)
plot_lm_4.set_figwidth(12)
plt.scatter(model_leverage, model_norm_residuals, alpha=0.5)
sns.regplot(model_leverage, model_norm_residuals,
scatter=False,
ci=False,
lowess=True,
line_kws={'color': 'red', 'lw': 1, 'alpha': 0.8})
plot_lm_4.axes[0].set_xlim(0, 0.20)
plot_lm_4.axes[0].set_ylim(-3, 5)
plot_lm_4.axes[0].set_title('Residuals vs Leverage')
plot_lm_4.axes[0].set_xlabel('Leverage')
plot_lm_4.axes[0].set_ylabel('Standardized Residuals')
# annotations
leverage_top_3 = np.flip(np.argsort(model_cooks), 0)[:3]
for i in leverage_top_3:
plot_lm_4.axes[0].annotate(i,
xy=(model_leverage[i],
model_norm_residuals[i]))
# shenanigans for cook's distance contours
def graph(formula, x_range, label=None, ls='-'):
x = x_range
y = formula(x)
plt.plot(x, y, label=label, lw=1, ls=ls, color='red')
p = len(model_fit.params) # number of model parameters
graph(lambda x: np.sqrt((0.5 * p * (1 - x)) / x),
np.linspace(0.001, 0.200, 50),
'Cook\'s distance = .5', ls='--') # 0.5 line
graph(lambda x: np.sqrt((1 * p * (1 - x)) / x),
np.linspace(0.001, 0.200, 50), 'Cook\'s distance = 1', ls=':') # 1 line
plt.legend(loc='upper right');
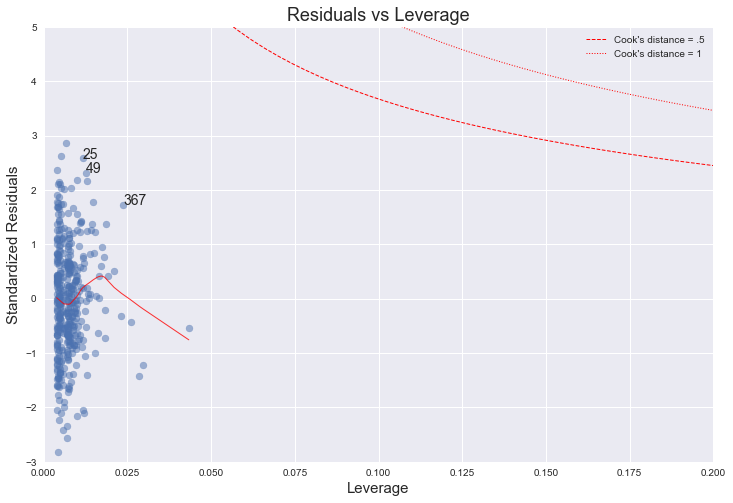
From this plot we can that no outliers (all less than 3). Since (p+1)/n=3/400=0.0075, we can see that there a few candidates for high leverage points, although every point is well below a Cook's distance of 1.
So on the whole this indicates that there are no outliers, but that there are some high leverage points although likely not very influential.